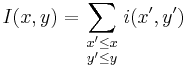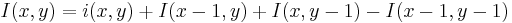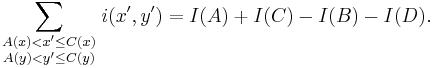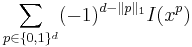Summed area table

A summed area table (also known as an integral image) is an algorithm for quickly and efficiently generating the sum of values in a rectangular subset of a grid. It was first introduced to the computer graphics world in 1984 for use in mipmaps but wasn't widely used in the computer vision community until its prominent use in the Viola–Jones object detection framework twenty years later.

1 The algorithm
2 Extensions
3 Video Lectures
4 References

The algorithm

As the name suggests, the value at any point (x, y) in the summed area table is just the sum of all the pixels above and to the left of (x, y), inclusive:^[1]^[2]

$I(x,y) = \sum_{\begin{smallmatrix} x' \le x \\ y' \le y\end{smallmatrix}} i(x',y')$

Moreover, the summed area table can be computed efficiently in a single pass over the image, using the fact that the value in the summed area table at (x, y) is just:

$I(x,y) = i(x,y) %2B I(x-1,y) %2B I(x,y-1) - I(x-1,y-1)\,$

Once the summed area table has been computed, the task of evaluating any rectangle can be accomplished in constant time with just four array references. Specifically, using the notation in the figure at right, the value is just

$\sum_{\begin{smallmatrix} A(x) < x' \le C(x) \\ A(y) < y' \le C(y) \end{smallmatrix}} i(x',y') = I(A) %2B I(C) - I(B) - I(D).$

Extensions

This method is naturally extended to continuous domains ^[3].

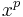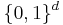The method can be also extended to high dimensional images^[4]. If the corners of the rectangle are $x^p$ with $p$ in $\{0,1\}^d$ , then the sum of image values contained in the rectagle are computed with the formula

$\sum_{p\in\{0,1\}^d }(-1)^{d-\|p\|_1} I(x^p) \,$

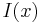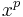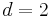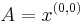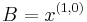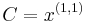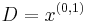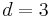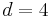where $I(x)$ is the integral image at $x$ and $d$ the image dimension. The notation $x^p$ correspond in the example to $d=2$ , $A=x^{(0,0)}$ , $B=x^{(1,0)}$ , $C=x^{(1,1)}$ and $D=x^{(0,1)}$ . In neuroimaging, for example, the images have dimension $d=3$ or $d=4$ , when using voxels or voxels with time-stamp.